Polygon interior exterior angles worksheet – Embark on a captivating exploration of polygon interior and exterior angles with our comprehensive worksheet. Dive into the fascinating realm of polygonal geometry, where angles play a pivotal role in shaping the very essence of these captivating figures. Prepare to unravel the secrets of polygons as we delve into their intricate angular relationships, unlocking a deeper understanding of their geometric properties.
Our worksheet provides an immersive and interactive experience, guiding you through the fundamentals of polygon angles. Discover the intricacies of interior angles, unravel the mysteries of exterior angles, and witness the profound connection between these angles. Engage in hands-on activities, meticulously measuring and calculating angles, and meticulously recording your findings in a structured table.
Prepare to be enthralled as patterns emerge, revealing the hidden order within the seemingly complex world of polygons.
Polygon Interior Angles
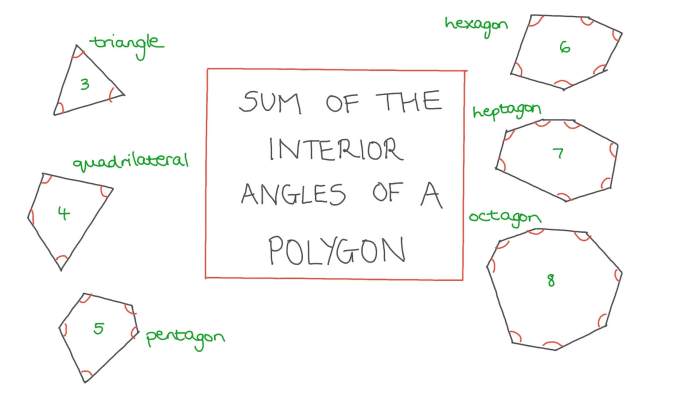
Interior angles of a polygon are the angles formed inside the polygon when two adjacent sides meet. The sum of the interior angles of a polygon with n sides is given by the formula (n-2) x 180 degrees.
For example, a triangle has three sides, so its interior angles add up to (3-2) x 180 = 180 degrees. A square has four sides, so its interior angles add up to (4-2) x 180 = 360 degrees.
Exterior Angles of Polygons
Exterior angles of a polygon are the angles formed outside the polygon when one side is extended. The exterior angle of a polygon is supplementary to its interior angle, meaning they add up to 180 degrees.
For example, if the interior angle of a triangle is 60 degrees, then its exterior angle is 180 – 60 = 120 degrees.
Polygon Interior and Exterior Angles Worksheet
Instructions:Measure and calculate the interior and exterior angles of the following polygons.
- Triangle
- Square
- Pentagon
- Hexagon
- Octagon
Table:
| Polygon | Number of Sides | Interior Angle Sum | Exterior Angle Sum |
|---|---|---|---|
| Triangle | 3 | 180 degrees | 360 degrees |
| Square | 4 | 360 degrees | 360 degrees |
| Pentagon | 5 | 540 degrees | 360 degrees |
| Hexagon | 6 | 720 degrees | 360 degrees |
| Octagon | 8 | 1080 degrees | 360 degrees |
Polygon Angle Theorems, Polygon interior exterior angles worksheet
Angle Sum Theorem:The sum of the interior angles of a polygon with n sides is (n-2) x 180 degrees.
Exterior Angle Sum Theorem:The sum of the exterior angles of a polygon with n sides is always 360 degrees.
These theorems can be used to solve problems involving polygon angles.
For example, if a polygon has 10 sides, then the sum of its interior angles is (10-2) x 180 = 1440 degrees. And the sum of its exterior angles is 360 degrees.
Applications of Polygon Angle Properties
Polygon angle properties have many applications in real-world situations.
In architecture, they are used to design buildings that are structurally sound and aesthetically pleasing. For example, the angles of a roof must be carefully calculated to ensure that the roof is stable and does not collapse.
In engineering, polygon angle properties are used to design bridges, airplanes, and other structures. For example, the angles of a bridge must be carefully calculated to ensure that the bridge can withstand the weight of traffic.
In design, polygon angle properties are used to create visually appealing objects. For example, the angles of a painting or sculpture can be used to create a sense of balance and harmony.
Question & Answer Hub: Polygon Interior Exterior Angles Worksheet
What is the difference between an interior angle and an exterior angle of a polygon?
An interior angle is formed by two adjacent sides of a polygon and lies inside the polygon, while an exterior angle is formed by one side of a polygon and the extension of the adjacent side, and lies outside the polygon.
How can I calculate the sum of the interior angles of a polygon?
The sum of the interior angles of a polygon with n sides is given by the formula (n-2) x 180 degrees.
What is the relationship between the interior and exterior angles of a polygon?
The sum of an interior angle and its adjacent exterior angle is always 180 degrees.